una desigualdad es una relación de orden que se da entre dos valores cuando éstos son distintos (en caso de ser iguales, lo que se tiene es una igualdad).
Signos de Desigualdad
x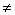 
y x no es igual a y.
y x no es igual a y.
Ejemplo: El número de días en una semana no es igual a 9.
x > y x es mayor que y. Ejemplo: 6 > 3
Ejemplo: El número de días en un mes es mayor que el número de días en una semana.
x < y x es menor que y.
Ejemplo: El número de días en una semana es menor que el número de días en un año.
x es mayor o igual a y.
Ejemplo: 31 es mayor o igual al número de días en un mes.
x es menor o igual a y.
Ejemplo: La velocidad legal de un carro en una zona de 25 mph es menor o igual a 25 mph.
Representando Desigualdades en la Recta Numérica
Las desigualdades se pueden graficar en la recta numérica. Abajo se muestran tres ejemplo de desigualdades y sus gráficas
x < 2
x ≤ −4
x ³ −3
AMPLIA LOS CONCEPTOS INGRESANDO A:
https://www.montereyinstitute.org/courses/DevelopmentalMath/TEXTGROUP-9-14_RESOURCE/U10_L2_T1_text_final_es.html
Una inecuación es una relación de desigualdad entre dos expresiones algebraicas en las que aparece una o más incógnitas. Resolver una inecuación consiste en encontrar todos los valores de la incógnita para los que se cumple la relación de desigualdad.
La solución de una inecuación es el conjunto de valores de la variable que verifica la inecuacíón.
Podemos expresar la solución de la inecuación mediante:
1. Una representación gráfica.
2. Un intervalo.
EJEMPLO:
2x − 1 ≤ 7
Solución gráfica
2x ≤ 8 x ≤ 4
Solución
La solución es el intervalo cerrado que va desde menos infinito a 4, tocando el punto, por eso va con corchete
x ∈ (-∞, 4]
INTERVALOSEs el conjunto de números reales comprendidos entre dos dados: ay b que se denominan extremos del intervalo. También se le llama intervalo al segmento determinado por los puntos a y b que se representa una porción de la recta real.
Los intervalos pueden ser cerrados o abiertos, según si incluyen (cerrados) o no (abiertos) sus extremos. Así,
- un intervalo abierto no incluye sus extremos; por ejemplo, es un intervalo abierto, ya que -2 y 3 no pertenecen a este intervalo.
- un intervalo cerrado incluye sus extremos; por ejemplo, es un intervalo cerrado, y -2 y 3 pertenecen a este intervalo.
- un intervalo abierto por un extremo no lo incluye, mientras que un intervalo cerrado por un extremo lo incluye. Por ejemplo, es un intervalo abierto por la derecha, y cerrado por la izquierda, ya que 3 no pertenece al intervalo, mientras que -2 sí que pertenece.
0 comentarios:
Publicar un comentario